Scopri tutto ciò che devi sapere sull’analisi esplorativa dei dati, un processo critico utilizzato per scoprire tendenze e modelli e riassumere i set di dati con l’aiuto di riepiloghi statistici e rappresentazioni grafiche.
Come ogni progetto, un progetto di data science è un processo lungo che richiede tempo, buona organizzazione e scrupoloso rispetto per diversi passaggi. L’analisi dei dati esplorativi (EDA) è uno dei passaggi più importanti di questo processo.
Pertanto, in questo articolo, esamineremo brevemente cos’è l’analisi esplorativa dei dati e come eseguirla con R!
Sommario:
Che cos’è l’analisi dei dati esplorativi?
L’analisi esplorativa dei dati esamina e studia le caratteristiche di un set di dati prima che venga inviato a un’applicazione, che sia esclusivamente aziendale, statistica o di machine learning.
Questo riassunto della natura dell’informazione e delle sue principali particolarità viene solitamente eseguito con metodi visivi, come rappresentazioni grafiche e tabelle. La pratica viene svolta in anticipo proprio per valutare le potenzialità di questi dati, che in futuro riceveranno un trattamento più complesso.
L’EDA consente quindi:
- Formulare ipotesi per l’utilizzo di queste informazioni;
- Esplora i dettagli nascosti nella struttura dei dati;
- Identificare valori mancanti, valori anomali o comportamenti anormali;
- Scopri le tendenze e le variabili rilevanti nel loro insieme;
- Scartare variabili irrilevanti o correlate ad altre;
- Determinare la modellazione formale da utilizzare.
Qual è la differenza tra l’analisi dei dati descrittiva ed esplorativa?
Esistono due tipi di analisi dei dati, analisi descrittiva e analisi esplorativa dei dati, che vanno di pari passo, pur avendo obiettivi diversi.
Mentre il primo si concentra sulla descrizione del comportamento di variabili, ad esempio media, mediana, moda, ecc.
L’analisi esplorativa mira a identificare le relazioni tra variabili, estrarre insight preliminari e indirizzare la modellazione verso i paradigmi di machine learning più comuni: classificazione, regressione e clustering.
In comune, entrambi possono occuparsi di rappresentazione grafica; tuttavia, solo l’analisi esplorativa cerca di portare intuizioni attuabili, cioè intuizioni che provocano l’azione del decisore.
Infine, mentre l’analisi esplorativa dei dati cerca di risolvere problemi e portare soluzioni che guideranno le fasi di modellazione, l’analisi descrittiva, come suggerisce il nome, mira solo a produrre una descrizione dettagliata del set di dati in questione.
Analisi descrittivaAnalisi esplorativa dei datiAnalizza il comportamentoAnalizza comportamento e relazioneFornisce un riepilogo Porta a specifiche e azioniOrganizza dati in tabelle e graficiOrganizza dati in tabelle e graficiNon ha un potere esplicativo significativoHa un potere esplicativo significativo
Alcuni casi di utilizzo pratico di EDA
# 1. Marketing digitale
Il marketing digitale si è evoluto da processo creativo a processo basato sui dati. Le organizzazioni di marketing utilizzano l’analisi dei dati esplorativi per determinare i risultati delle campagne o degli sforzi e per guidare gli investimenti dei consumatori e le decisioni di targeting.
Studi demografici, segmentazione dei clienti e altre tecniche consentono agli esperti di marketing di utilizzare grandi quantità di dati sugli acquisti, sondaggi e panel dei consumatori per comprendere e comunicare strategie di marketing.
L’analisi esplorativa Web consente agli esperti di marketing di raccogliere informazioni a livello di sessione sulle interazioni su un sito Web. Google Analytics è un esempio di uno strumento di analisi gratuito e popolare utilizzato dai marketer per questo scopo.
Le tecniche esplorative frequentemente utilizzate nel marketing includono la modellazione del marketing mix, l’analisi dei prezzi e delle promozioni, l’ottimizzazione delle vendite e l’analisi esplorativa dei clienti, ad esempio la segmentazione.
#2. Analisi esplorativa del portafoglio
Un’applicazione comune dell’analisi esplorativa dei dati è l’analisi esplorativa del portafoglio. Una banca o un’agenzia di prestito ha una collezione di conti di valore e rischio variabili.
I conti possono differire a seconda dello stato sociale del titolare (ricco, ceto medio, povero, ecc.), della posizione geografica, del patrimonio netto e di molti altri fattori. Il prestatore deve bilanciare il rendimento del prestito con il rischio di insolvenza per ogni prestito. La domanda quindi diventa come valutare il portafoglio nel suo insieme.
Il prestito a più basso rischio può essere per persone molto facoltose, ma c’è un numero molto limitato di persone benestanti. D’altra parte, molti poveri possono prestare, ma a maggior rischio.
La soluzione di analisi dei dati esplorativa può combinare l’analisi delle serie temporali con molti altri problemi per decidere quando prestare denaro a questi diversi segmenti di mutuatari o il tasso di prestito. Gli interessi vengono addebitati ai membri di un segmento di portafoglio per coprire le perdite tra i membri di quel segmento.
#3. Analisi esplorativa del rischio
Sono in fase di sviluppo modelli predittivi nel settore bancario per fornire certezza sui punteggi di rischio per i singoli clienti. I punteggi di credito sono progettati per prevedere il comportamento delinquente di un individuo e sono ampiamente utilizzati per valutare l’affidabilità creditizia di ciascun richiedente.
Inoltre, l’analisi del rischio viene svolta nel mondo scientifico e nel settore assicurativo. È anche ampiamente utilizzato nelle istituzioni finanziarie come le società di gateway di pagamento online per analizzare se una transazione è genuina o fraudolenta.
A tale scopo, utilizzano la cronologia delle transazioni del cliente. È più comunemente usato negli acquisti con carta di credito; quando si verifica un picco improvviso nel volume delle transazioni del cliente, il cliente riceve una chiamata di conferma se ha avviato la transazione. Aiuta anche a ridurre le perdite dovute a tali circostanze.
Analisi dei dati esplorativi con R
La prima cosa di cui hai bisogno per eseguire EDA con R è scaricare R base e R Studio (IDE), quindi installare e caricare i seguenti pacchetti:
#Installing Packages
install.packages("dplyr")
install.packages("ggplot2")
install.packages("magrittr")
install.packages("tsibble")
install.packages("forecast")
install.packages("skimr")
#Loading Packages
library(dplyr)
library(ggplot2)
library(magrittr)
library(tsibble)
library(forecast)
library(skimr)
Per questo tutorial, utilizzeremo un set di dati economici integrato con R e fornisce dati annuali sugli indicatori economici dell’economia statunitense e cambieremo il suo nome in econ per semplicità:
econ <- ggplot2::economics
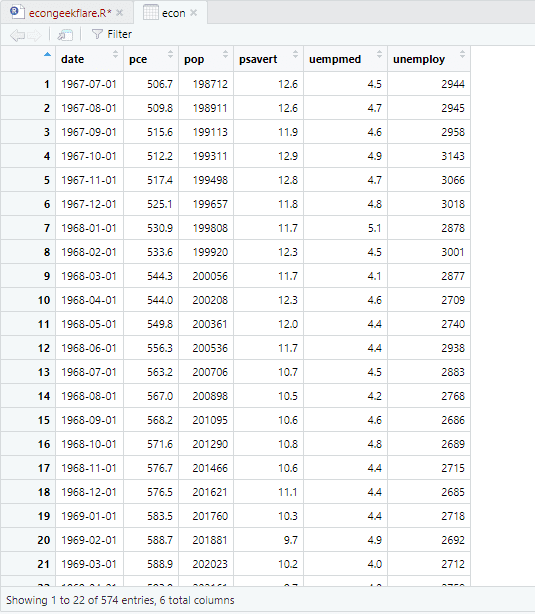
Per eseguire l’analisi descrittiva utilizzeremo il pacchetto skimr, che calcola queste statistiche in modo semplice e ben presentato:
#Descriptive Analysis skimr::skim(econ)

È inoltre possibile utilizzare la funzione di riepilogo per l’analisi descrittiva:
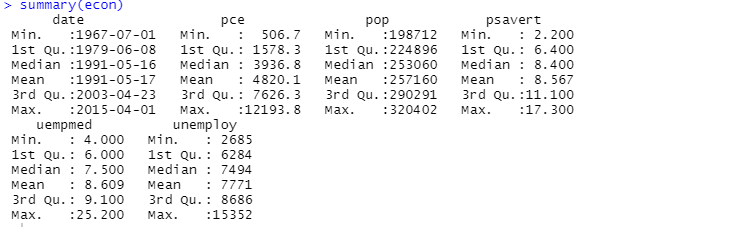
Qui l’analisi descrittiva mostra 547 righe e 6 colonne nel set di dati. Il valore minimo è per 1967-07-01 e il massimo è per 2015-04-01. Allo stesso modo, mostra anche il valore medio e la deviazione standard.
Ora hai un’idea di base di cosa c’è all’interno del set di dati econ. Tracciamo un istogramma della variabile uempmed per osservare meglio i dati:
#Histogram of Unemployment econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Unemployment", title = "Monthly Unemployment Rate in US between 1967 to 2015")
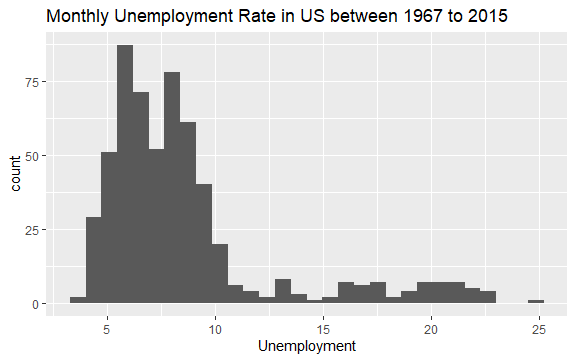
La distribuzione dell’istogramma mostra che ha una coda allungata a destra; cioè, ci sono forse alcune osservazioni di questa variabile con valori più “estremi”. Sorge la domanda: in che periodo si sono verificati questi valori, e qual è l’andamento della variabile?
Il modo più diretto per identificare l’andamento di una variabile è attraverso un grafico a linee. Di seguito generiamo un grafico a linee e aggiungiamo una linea di levigatura:
#Line Graph of Unemployment econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth()
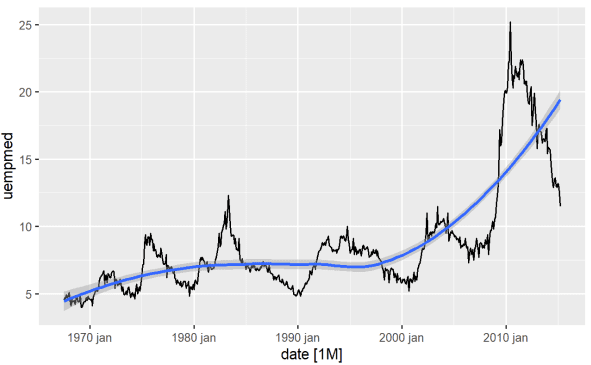
Utilizzando questo grafico, possiamo identificare che nel periodo più recente, nelle ultime osservazioni del 2010, c’è una tendenza all’aumento della disoccupazione, superando la storia osservata nei decenni precedenti.
Un altro punto importante, soprattutto in contesti di modellizzazione econometrica, è la stazionarietà della serie; cioè, la media e la varianza sono costanti nel tempo?
Quando queste ipotesi non sono vere in una variabile, diciamo che la serie ha una radice unitaria (non stazionaria) in modo che gli shock che subisce la variabile generino un effetto permanente.
Sembra sia stato il caso della variabile in questione, la durata della disoccupazione. Abbiamo visto che le fluttuazioni della variabile sono cambiate considerevolmente, il che ha forti implicazioni legate alle teorie economiche che si occupano di cicli. Ma, partendo dalla teoria, come si verifica in pratica se la variabile è stazionaria?
Il pacchetto di previsione ha un’ottima funzione che consente di applicare test, come ADF, KPSS e altri, che già restituiscono il numero di differenze necessarie affinché la serie sia stazionaria:
#Using ADF test for checking stationarity forecast::ndiffs( x = econ$uempmed, test = "adf")

Qui il valore p maggiore di 0,05 mostra che i dati non sono stazionari.
Un’altra questione importante nelle serie temporali è l’identificazione di possibili correlazioni (la relazione lineare) tra i valori ritardati della serie. I correlogrammi ACF e PACF aiutano a identificarlo.
Poiché la serie non ha stagionalità ma ha una certa tendenza, le autocorrelazioni iniziali tendono ad essere ampie e positive perché anche le osservazioni che si chiudono nel tempo hanno un valore vicino.
Pertanto, la funzione di autocorrelazione (ACF) di una serie temporale con trend tende ad avere valori positivi che diminuiscono lentamente all’aumentare dei ritardi.
#Residuals of Unemployment checkresiduals(econ$uempmed) pacf(econ$uempmed)
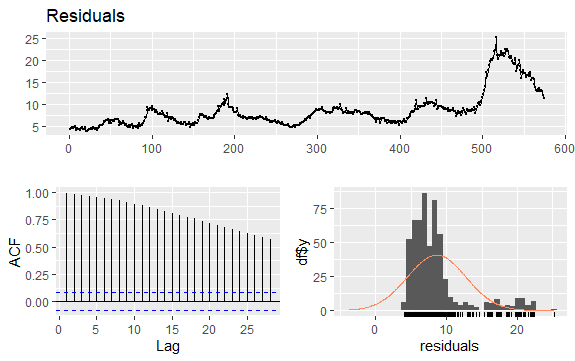
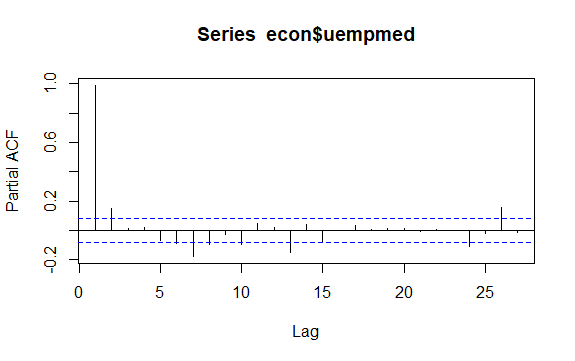
Conclusione
Quando mettiamo le mani su dati più o meno puliti, cioè già puliti, siamo subito tentati di tuffarci nella fase di costruzione del modello per trarre i primi risultati. Devi resistere a questa tentazione e iniziare a fare analisi esplorative dei dati, che è semplice ma ci aiuta a trarre potenti intuizioni nei dati.
Puoi anche esplorare alcune delle migliori risorse per apprendere le statistiche per la scienza dei dati.
